Exercício Resolvido de Dinâmica
publicidade
Sobre um plano inclinado de 30° em relação à horizontal, desliza sem atrito uma massa
m1 presa a uma outra massa m2. Abandonando o sistema a partir do
repouso a massa m2 sobe 250 m em 20 s. Calcular a relação
m1/m2. Adote g = 10 m/s2.
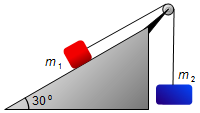
Dados do problema:
- Massa do bloco 1: m1;
- Ângulo de inclinação do plano: θ = 30°;
- Massa do bloco 2: m2;
- Deslocamento do bloco 2: ΔS = 250 m;
- Velocidade inicial do sistema: v0 = 0;
- Intervalo de tempo de subida: Δt = 20 s
- Aceleração da gravidade: g = 10 m/s2.
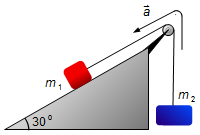
Adotamos a aceleração do sistema no sentido do bloco de massa m1 descendo o plano e a
massa m2 subindo (Figura 1).
Solução
Isolamos os corpos e pesquisamos as forças que atuam em cada um deles.
Bloco 1 (Figura 2-A):
Adotamos um sistema de referência xy com eixo-x na direção do plano inclinado e sentido descendente. Neste corpo atuam a força peso do bloco 1 \( {\vec P}_{1} \), a força normal de reação do plano sobre o bloco 1 \( {\vec N}_{1} \) e a força de tensão na corda \( \vec{T} \).
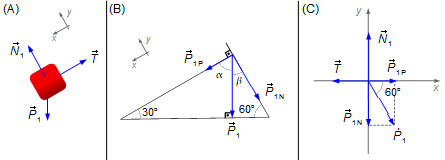
A força peso \( {\vec{P}}_{1} \) pode ser decomposta em duas, uma componente paralela ao eixo-x \( {\vec P}_{1P} \) e a outra componente normal ou perpendicular \( {\vec P}_{1N} \).
No triângulo à esquerda na Figura 2-B a força peso é perpendicular ao plano horizontal, forma um ângulo de 90°, o ângulo entre o plano inclinado e o plano horizontal é dado como 30°, como os ângulos internos de um triângulo devem somar 180°, o ângulo α entre a força peso e a componente paralela deve ser
\[
\alpha +30°+90°=180°\Rightarrow \alpha=180°-30°-90°\Rightarrow \alpha=60°
\]
No triângulo à direita, a componente normal faz com o plano inclinado um ângulo de 90°, então o ângulo β
entre a força peso e a componente normal deve ser
\[
\alpha+\beta=90° \Rightarrow \beta =90°-\alpha \Rightarrow 90°-60°\Rightarrow 30°
\]
Desenhamos as forças em um sistema de eixos coordenados xy (Figura 2-C) e aplicamos a 2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}} \tag{I}
\end{gather}
\]
Na direção y não há movimento, a força normal de reação
\( {\vec N}_{1} \)
e a componente normal do peso
\( {\vec P}_{1N} \)
se anulam.Direção x:
\[
\begin{gather}
P_{1P}-T=m_{1}a \tag{II}
\end{gather}
\]
a componente do peso na direção paralela é dada por (Figura 2-C)
\[
\begin{gather}
P_{1P}=P_{1}\cos 60° \tag{III}
\end{gather}
\]
a força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{IV}
\end{gather}
\]
para o bloco m1 a força peso é dada por
\[
\begin{gather}
P_{1}=m_{1}g \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (III)
\[
\begin{gather}
P_{1P}=m_{1}g\cos 60° \tag{VI}
\end{gather}
\]
e substituindo a expressão (VI) na expressão (II)
\[
\begin{gather}
m_{1}g\cos 60°-T=m_{1}a \tag{VII}
\end{gather}
\]
Bloco 2 (Figura 3):
- \( {\vec P}_{2} \): força peso do bloco 2;
- \( \vec{T} \): força de tensão na corda.

Figura 3
Adotamos o sentido positivo para cima no mesmo sentido da aceleração. Na direção horizontal não há forças atuando no bloco, na direção vertical aplicando a expressão (I)
\[
\begin{gather}
T-P_{2}=m_{2}a \tag{VIII}
\end{gather}
\]
Para o bloco m2 a força peso é dada por
\[
\begin{gather}
P_{2}=m_{2}g \tag{IX}
\end{gather}
\]
substituindo a expressão (IX) n expressão (VIII)
\[
\begin{gather}
T-m_{2}g=m_{2}a \tag{X}
\end{gather}
\]
Somando as expressões (VII) e (X) temos a aceleração do sistema
\[
\frac{
\begin{matrix}
m_{1}g\cos 60°-\cancel{T}=m_{1}a\\
\text{(+)}\qquad\quad\;\cancel{T}-m_{2}g=m_{2}a \quad\;
\end{matrix}}
{m_{1}g\cos 60°-m_{2}g=m_{1}a+m_{2}a}
\]
colocando a aceleração da gravidade g em evidência do lado esquerdo da igualdade e a aceleração
a do lado direito
\[
\begin{gather}
g(m_{1}\cos 60°-m_{2})=a(m_{1}+m_{2})\\[5pt]
a=g\left(\frac{m_{1}\cos 60°-m_{2}}{m_{1}+m_{2}}\right) \tag{XI}
\end{gather}
\]
Da Cinemática Escalar usamos a equação horária do Movimento Retilíneo Uniformemente Variado
(M.R.U.V.)
\[ \bbox[#99CCFF,10px]
{S=S_{0}+V_{0}t+\frac{a}{2}t^{2}}
\]
\[
S-S_{0}=V_{0}t+\frac{a}{2}t^{2}
\]
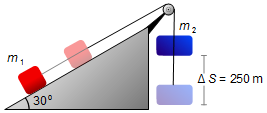
sendo \( \Delta S=S-S_{0} \) e usando o valor da aceleração da expressão (XI)
\[
\Delta S=V_{0}t+\frac{1}{2}g\left(\frac{m_{1}\cos 60°-m_{2}}{m_{1}+m_{2}}\right)t^{2}
\]
Lembrando da Trigonometria
\[
\cos 60°=\dfrac{1}{2}
\]
Substituindo os valores dados no problema e sendo \( \Delta t=t-t_{0}\Rightarrow 20=t-0\Rightarrow t=20\;\text{s, } \)
\( \Delta t=t-t_{0}\Rightarrow 20=t-0\Rightarrow t=20\;\text{s, } \)
\[
\begin{gather}
250=0.20+\frac{1}{2}.10.\left(\frac{m_{1}\dfrac{1}{2}-m_{2}}{m_{1}+m_{2}}\right).20^{2}\\[5pt]
250=0+5.\left(\frac{\dfrac{m_{1}-2m_{2}}{2}}{m_{1}+m_{2}}\right).400\\[5pt]
250=\left[\frac{m_{1}-2m_{2}}{2\left(m_{1}+m_{2}\right)}\right].2000\\[5pt]
\frac{250}{2000}=\frac{m_{1}-2m_{2}}{2m_{1}+2m_{2}}
\end{gather}
\]
do lado esquerdo da igualdade dividimos o numerador e o denominador por 250
\[
\begin{gather}
\frac{250:250}{2000:250}=\frac{m_{1}-2m_{2}}{2m_{1}+2m_{2}}\\[5pt]
\frac{1}{8}=\frac{m_{1}-2m_{2}}{2m_{1}+2m_{2}}
\end{gather}
\]
multiplicando em “cruz”
\[
\begin{gather}
2m_{1}+2m_{2}=8.\left(m_{1}-2m_{2}\right)\\[5pt]
2m_{1}+2m_{2}=8m_{1}-16m_{2}\\[5pt]
2m_{2}+16m_{2}=8m_{1}-2m_{1}\\[5pt]
18m_{2}=6m_{1}\\[5pt]
\frac{m_{1}}{m_{2}}=\frac{18}{6}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\frac{m_{1}}{m_{2}}=3}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .