Exercício Resolvido de Centro de Massa
EN
ES
FR
publicidade
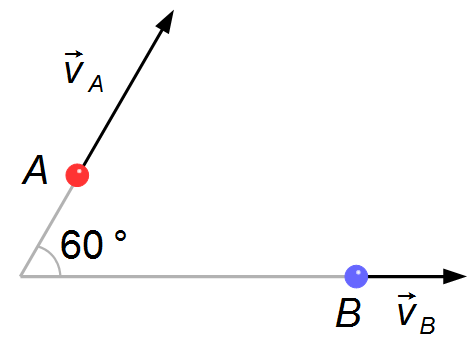
Duas partículas A e B têm massas respectivamente iguais a 4 kg e 6 kg. Ambas movem-se com
velocidades constantes va = 5 m/s e vb = 3 m/s tais que suas
direções formam um ângulo de 60°. Determine:
a) A velocidade do centro de massa;
b) A quantidade de movimento do sistema.
a) A velocidade do centro de massa;
b) A quantidade de movimento do sistema.
Dados do problema:
- Massa da partícula A: ma = 4 kg;
- Massa da partícula B: mb = 6 kg;
- Velocidade da partícula A: va = 5 m/s;
- Velocidade da partícula B: vb = 3 m/s.
Solução:
a) A velocidade do centro de massa será dada pela seguinte equação na forma vetorial
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec v=\frac{m_a{\vec v}_a+m_b{\vec v}_b}{m_a+m_b}}
\end{gather}
\]
na forma escalar está equação pode ser decomposta nas direções x e y
\[
\begin{gather}
v_x=\frac{m_av_{ax}+m_bv_{bx}}{m_a+m_b} \tag{I-a}
\end{gather}
\]
\[
\begin{gather}
v_y=\frac{m_av_{ay}+m_bv_{by}}{m_a+m_b} \tag{I-b}
\end{gather}
\]
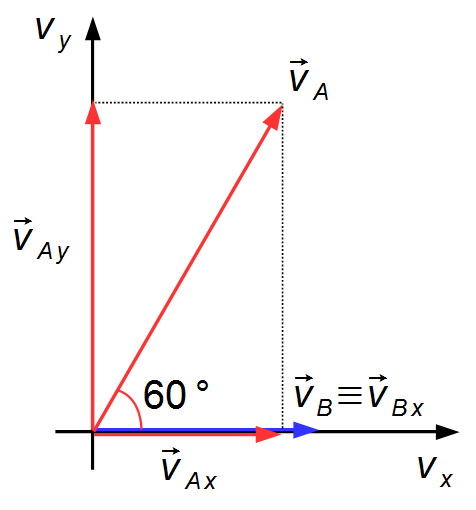
Desenhamos os vetores velocidades
\( {\vec v}_a \)
e
\( {\vec v}_b \)
em um sistema de eixos cartesianos, e obtemos suas componentes, o vetor velocidade
\( {\vec v}_b \)
coincide com o eixo-x, então o ângulo entre eles será 0° (Figura 1)
- Direção horizontal:
\[
\begin{gather}
v_{ax}=v_a\cos 60°
\end{gather}
\]
Da Trigonometria
\( \cos 60°=\dfrac{1}{2} \)
\[
\begin{gather}
v_{ax}=5\times\frac{1}{2} \\[5pt]
v_{ax}=2,5\;\mathrm{m/s} \tag{II}
\end{gather}
\]
\[
\begin{gather}
v_{bx}=v_b\cos 0°
\end{gather}
\]
Da Trigonometria
\( \cos 0°=1 \)
\[
\begin{gather}
v_{bx}=3\times 1 \\[5pt]
v_{bx}=3\;\mathrm{m/s} \tag{III}
\end{gather}
\]
- Direção vertical:
\[
\begin{gather}
v_{ay}=v_a\operatorname{sen}60°
\end{gather}
\]
Da Trigonometria
\( \operatorname{sen}60°=\dfrac{\sqrt{3\;}}{2} \)
\[
\begin{gather}
v_{ay}=5\times\frac{\sqrt{3\;}}{2} \\[5pt]
v_{ay}=4,3\;\mathrm{m/s} \tag{IV}
\end{gather}
\]
\[
\begin{gather}
v_{by}=v_b\operatorname{sen}0°
\end{gather}
\]
Da Trigonometria
\( \operatorname{sen}0°=0 \)
\[
\begin{gather}
v_{by}=3\times 0 \\[5pt]
v_{by}=0 \tag{V}
\end{gather}
\]
Substituindo os valores das massas e as velocidades (II) e (III) na direção x na expressão (I-a)
\[
\begin{gather}
v_x=\frac{4\times 2,5+6\times 3}{4+6} \\[5pt]
v_x=\frac{10+18}{10} \\[5pt]
v_x=2,8\;\mathrm{m/s} \tag{VI}
\end{gather}
\]
Substituindo os valores das massas e as velocidades (IV) e (V) na direção y na expressão (I-b)
\[
\begin{gather}
v_y=\frac{4\times 4,3+6\times 0}{4+6} \\[5pt]
v_y=\frac{17,2+0}{10} \\[5pt]
v_y=1,7\;\mathrm{m/s} \tag{VII}
\end{gather}
\]
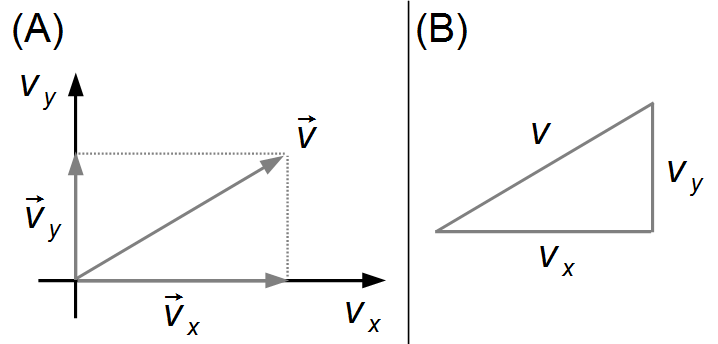
Os vetores
\( {\vec v}_x \)
e
\( {\vec v}_y \)
estão representados na Figura 2-A e sua soma vetorial nos dará o vetor velocidade do centro de massa do
sistema. O módulo deste vetor pode ser encontrado aplicando-se o Teorema de Pitágoras ao triângulo
retângulo da Figura 2-B, onde os catetos representam as velocidades nas direções x e y, e
a hipotenusa a velocidade do centro de massa.
\[
\begin{gather}
v^2=v_x^2+v_y^2
\end{gather}
\]
substituindo os resultados (VI) e (VII) para as velocidades
\[
\begin{gather}
v^2=(2,8)^2+(1,7)^2 \\[5pt]
v^2=7,84+2,89 \\[5pt]
v^2=10,73 \\[5pt]
v=\sqrt{10,73\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=3,3\;\mathrm{m/s}}
\end{gather}
\]
b) A quantidade de movimento do sistema será
\[
\begin{gather}
\bbox[#99CCFF,10px]
{Q=mv}
\end{gather}
\]
onde m é a massa total do sistema.
\[
\begin{gather}
Q=(m_a+m_b)v \\[5pt]
Q=(4+6)\times 3,3
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{Q=33\;\mathrm{kg.m/s}}
\end{gather}
\]
publicidade