Um fio com área de seção transversal 0,50×10−2 cm2, é percorrido por uma
corrente contínua de intensidade igual a 4,0 A. Dada a carga elementar 1,6×10−19 C,
determinar:
a) O número de elétrons passando por uma seção transversal por segundo;
b) A velocidade média dos elétrons, sabendo que existem 1,8.1020 elétrons/cm3.
Dados do problema:
- Área transversal do fio: A = 0,50×10−2cm2;
- Corrente elétrica: i = 4,0 A;
- Carga elementar: e = 1,6×10−19 C.
Solução:
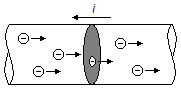
a) Na Figura 1 os elétrons se deslocam atravessando uma seção transversal, destacada em cinza. A corrente
elétrica é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{i=\frac{\Delta q}{\Delta t}} \tag{I}
\end{gather}
\]
A quantidade de carga que atravessa uma determinada seção é dada por
\[
\begin{gather}
\Delta q=n{\mathrm e} \tag{II}
\end{gather}
\]
substituindo a equação (II) na equação (I)
\[
\begin{gather}
i=\frac{n{\mathrm e}}{\Delta t} \\[5pt]
n=\frac{i\Delta t}{\mathrm e}
\end{gather}
\]
substituindo os dados do problema para Δt = 1 s
\[
\begin{gather}
n=\frac{4\times 1}{1,6\times 10^{-19}} \\[5pt]
n=\frac{4\times 10^{19}}{1,6}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{n=2,5\times 10^{19}\;\text{elétrons}}
\end{gather}
\]
b) A velocidade média é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_m=\frac{\Delta S}{\Delta t}} \tag{III}
\end{gather}
\]
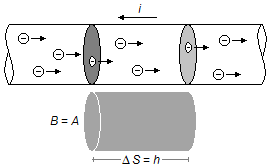
então um elétron que passe pela seção transversal do fio num determinado instante vai percorrer
uma distância Δ
S num intervalo de tempo Δ
t, o elétron passa então por
uma outra seção transversal. Estas duas seções transversais determinam um cilindro no fio de
volume
V dado por (Figura 2)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V=Bh} \tag{IV}
\end{gather}
\]
onde B é a área da base do cilindro, área da seção transversal do fio B = A,
e h é o deslocamento do elétron, h = ΔS, substituindo esses valores na
equação (IV)
\[
\begin{gather}
V=A \Delta S \\[5pt]
\Delta S=\frac{V}{A} \tag{V}
\end{gather}
\]
substituindo a equação (V) na equação (III)
\[
\begin{gather}
v_m=\frac{V}{A\Delta t} \tag{VI}
\end{gather}
\]
A densidade volumétrica de cargas d é dada por
\[
\begin{gather}
d=\frac{n}{V}
\end{gather}
\]
onde n é o número de elétrons contidos no volume V do cilindro determinado pelas duas
seções transversais no fio
\[
\begin{gather}
V=\frac{n}{d} \tag{VII}
\end{gather}
\]
substituindo a equação (VII) na equação (VI)
\[
\begin{gather}
v_m=\frac{n}{dA\Delta t}
\end{gather}
\]
Usando os dados do problema, o valor de n calculado no item anterior e sendo a velocidade
calculada por unidade de tempo temos Δt = 1 s
\[
\begin{gather}
v_m=\frac{2,5\times 10^{19}}{1,8\times 10^{20}\times 0,50\times 10^{-2}\times 1} \\[5pt]
v_m=\frac{2,5\times 10^{19}}{9\times 10^{17}} \\[5pt]
v_m=\frac{2,5\times 10^{19}\times 10^{-17}}{9} \\[5pt]
v_m=0,28\times 10^2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_m=28\;\mathrm{cm/s}}
\end{gather}
\]
EN
