Exercício Resolvido de Dinâmica
publicidade   

Um homem de massa m = 70 kg, está em um elevador, este se move com aceleração a = 2 m/s2. Determinar:
a) A força com que o homem atua no piso do elevador, se o elevador está descendo;
b) A força com que o homem atua no piso do elevador, se o elevador está subindo;
c) Para qual aceleração do elevador a força do homem sobre o piso do elevador será igual a zero?

 

Dados do problema:

  • Massa do homem:    m = 70 kg;
  • Aceleração do elevador:    a = 2 m/s2;
  • Aceleração da gravidade:    g = 9,8 m/s2.

Solução:

a) Adotamos um sistema de referência orientado para a baixo, no mesmo sentido da aceleração do elevador.
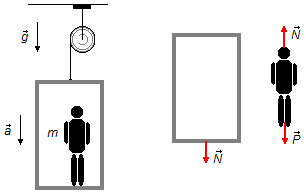
Fazendo um Diagrama de Corpo Livre, temos as forças que atuam nos corpos (Figura 1).

  • Elevador:
    • \( \vec N \): ação do homem sobre o piso do elevador.
  • Homem:
    • \( \vec P \): força peso do homem.
    • \( \vec N \): força de reação do piso do elevador sobre o homem.
Figura 1
Observação: No elevador também existe o peso do próprio elevador. Mas como desejamos encontrar a força que o homem faz sobre o elevador e esta é igual, em módulo, à reação do elevador sobre o homem, \( \vec N \), basta analisar as forças que atuam no homem.

Aplicando a 2.ª Lei de Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Homem:
\[ \begin{gather} P-N=ma \tag{I} \end{gather} \]

a força peso é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]

substituindo esta equação na equação (I)

\[ \begin{gather} mg-N=ma \\[5pt] N=m\;(g-a) \tag{II} \\[5pt] N=70\times(9,8-2) \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {N=546\;\mathrm N} \end{gather} \]

 

b) Adotamos um sistema de referência orientado para a cima, no mesmo sentido da aceleração do elevador.
Novamente, fazendo um Diagrama de Corpo Livre, temos as forças que atuam nos corpos (Figura 2) e podemos aplicar a 2.ª Lei de Newton.
As forças que atuam no elevador e no homem são as mesmas do item (a), (Figuras 1 e 2).

Figura 2

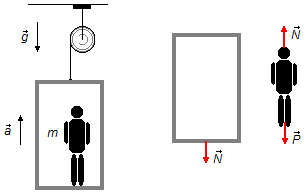
Aplicando a equação (I) ao homem, considerando agora a inversão no sentido da aceleração do elevador

\[ \begin{gather} N-mg=ma \\[5pt] N=m\;(g+a) \tag{III} \\[5pt] N=70\times(9,8+2) \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {N=826\;\mathrm N} \end{gather} \]

 

c) Se o homem não exerce força no piso do elevador, devemos ter a força normal nula, N = 0. Substituindo esta condição na equação (II) do item (a)

\[ \begin{gather} 0=m\;(g-a) \\[5pt] g-a=\frac{0}{m} \\[5pt] g-a=0 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a=g=9,8\;\mathrm{m/s^2}} \end{gather} \]
Observação 1: Este resultado significa que o elevador e o homem estão em queda livre. O homem tende a “descolar” do chão do elevador, não há ação do homem sobre o elevador e não há reação do elevador sobre o homem.

Observação 2: Se ao invés de utilizarmos a equação (II) do item (a), tivéssemos usado a equação (III) do item (b), com a condição de N = 0, o resultado seria a = −g. Isto significa que o módulo da aceleração seria o mesmo, mas o sentido da aceleração, que no item (b) está orientada para cima, teria que ser invertida para baixo, o que faz coincidir com a situação do item (a).
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .