Dois corpos de massas m_a = 6 kg e m_b = 4 kg estão sobre uma superfície horizontal perfeitamente lisa. Uma força horizontal de intensidade igual a 25 N é aplicada de forma a empurrar os dois corpos. Calcule a aceleração adquirida pelo conjunto e o intensidade da força de contato entre os corpos.

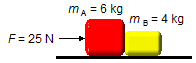
Dados do problema:

• Massa do corpo A:    m_a = 6 kg;
• Massa do corpo B:    m_b = 4 kg;
• Força aplicada ao conjunto:    F = 25 N.

Esquema do problema:

Adotamos um sistema de referência orientado para a direita no mesmo sentido da força \( \vec F \) aplicada, esta produz uma aceleração a no sistema.

Figura 1

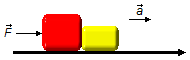
Fazendo um Diagrama de Corpo Livre temos as forças que atuam nos blocos.

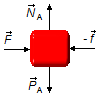
• Corpo A:
  • Direção horizontal:
    • \( \vec F \) : força aplica ao corpo;
    • \( -\vec f \) : força de reação do corpo B em A.
  • Direção vertical:
    • \( {\vec N}_a \) : força de reação normal da superfície no corpo;
    • \( {\vec P}_a \) : peso do corpo A.

Figura 2

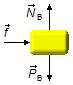
• Corpo B:
  • Direção horizontal:
    • \( \vec f \): força de ação do corpo A em B.
  • Direção vertical:
    • \( {\vec N}_b \): força de reação normal da superfície no corpo;
    • \( {\vec P}_b \): peso do corpo B.

Figura 3

Solução:

Aplicando a 2.ª Lei de Newton

• Corpo A:

Na direção vertical não há movimento, a força normal e a força peso se anulam.
Na direção horizontal

• Corpo B:

Na direção vertical não há movimento, a força normal e a força peso se anulam.
Na direção horizontal

As equações (I) e (II) formam um sistema de duas equações a duas incógnitas (f e a)

substituindo a equação (II) na equação (I) obtemos a aceleração

Substituindo a aceleração encontrada acima na equação (II) temos a força de contato entre os corpos